Terdapat 3 metode yang
digunakan secara luas untuk memisahkan biaya campuran menjadi komponen tetap
dan variabel, yaitu :
1.
Metode Tinggi Rendah
2.
Metode Scatterplot
3.
Metode Kuadrat Terkecil
Setiap metode menghendaki kita membuat asumsi
penyederhanaan hubungan biaya linear. Biaya – biaya campuran dianggap mengikuti
hubungan linear berikut :
Y
= F + VX
|
Y = total biaya aktivitas ( variabel
tidak bebas )
F
= komponen biaya tetap ( parameter titik potong )
X = ukuran keluaran aktivitas ( variabel
bebas )
V = biaya variabel / unit aktivitas.
Karena catatan akuntansi hanya menyatakan X
dan Y maka nilai – nilai tersebut harus digunakan untuk mengestimasi parameter
F dan V, dengan begitu komponen tetap dan variabel dapat diestimasi dan
perilaku biaya campuran dapat diperediksi ketika penggunaan aktivitas berubah.
1.
Metode
Tinggi Rendah.
Pada
metode ini, dua titik yang dipilih dari scattergraph adalah titik tertinggi dan
titik terendah berkenaan dengan tingkat aktivitas. Dua titik ini kemudian
digunakan untuk menghitung titik potong dan kemiringan garis dimana kedua titik
tersebut terletak.
Persamaan
untuk menentukan kemiringan dan perpotongan adalah sebagai berikut :
V
= Perubahan_biaya = ( Y2 – Y1 )
Perubahan
aktivitas ( X2 – X1 )
F
= Total biaya campuran – biaya variabel = Y2 – VX2 atau Y1 – VX1
2.
Metode
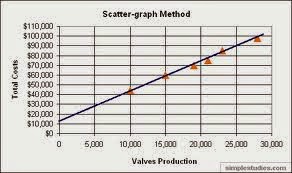
Scatterplot
Pada metode ini menyangkut pemeriksaan scattergraph
dan pemilihan dua titik yang tampaknya terbaik untuk mewakili hubungan antara
biaya dan aktivitas.
Langkah pertama dalam metode ini kita
harus memplot titik data sehingga hubungan antara biaya persiapan dan tingkat
aktivitas dapat terlihat.
3.
Metode Kuadrat
Terkecil
Metode ini menggunakan semua tititk data
pada scattergraph dan menghasilkan suatu garis terbaik untuk semua titik. Garis
terbaik adalah garis yang terdekat ke semua titik yang diukur melalui
penjumlahan kuadrat deviasi titik – titik tersebut dari garis.
Garis yang lebih mendekati titik
dibandingkan garis yang lainnya disebut garis kecocokan terbaik yaitu garis dengan
jumlah kuadrat deviasi terkecil.
Rumus untuk menghasilkan garis terbaik :
( ∑XY - ∑X ∑Y /
n )
V = ---------------------------
( ∑X2 – ( ∑X )2 / n )
∑Y ∑X
F = ------ - V
--------
n n
Persentase variabilitas variabel tidak
bebas yang dijelaskan oleh suatu variabel bebas disebut koefisien determasi. Seamakin tinggi persentase variabelitas yang
diterangkan semakin baik garisnya. Nilainya berkisar 0 – 1 koefisien determasi
diberi tanda R2.
V ( ∑XY - ∑X ∑Y / n
)
R = -----------------------------
( ∑Y2 – ( ∑Y )2 / n )
Koefisien
Relasi adalah
akar dari koefisien determasi. Nilai koefisien korelasi – 1 dan +1
Untuk contoh soal dan jawabannya. klik : Disini







No comments:
Post a Comment
Sebagai pengunjung blog yg baik jgn lupa y tinggalkan komentar, saran atau y itu gak usah dibilang agan2 semua tau kan, agar blog ini bisa terus memberikan informasi pada agan - agan semua.